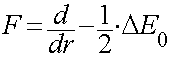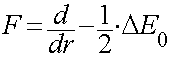
Nach Meinung eines Kritikers der Relativitätstheorie Albert Einsteins, Dipl.-Ing. (FH) Walter Orlov, rechnete Einstein die rel. Periheldrehung des Merkurs so, als ob sich die Sonne um den Merkur drehe. Orlovs daraufhin durchgeführte sog. vollständige Berechnung des relativistischen Anteils der Periheldrehung des Merkurs ergibt dann auch nicht die 43,03 Bogensekunden, wie von Einstein ermittelt und welche so ideal die Diskrepanz zwischen der experimentellen Messung und der Auffassung nach Newton schließt, sondern ~50“ (s. Anlage 2).
Diese 7“ zuviel könnten jedoch haltlos sein. In Anlage 1 wird gezeigt, dass die Schwerkraft ein Produkt aus der Veränderung der Ruheenergie von Massen gegenüber dem Off ist, welche sich aus der Zeitdehnung ableitet, ähnlich wie auch die Relativitätstheorie Einsteins bzw. seine Schwerkraftauffassung auf der Zeitdehnung fußt. Das Ergebnis ist eine Modifikation des Schwerkraftausdrucks nach Newton mit einem Term, der jedoch negativ ist. Damit besteht die Möglichkeit einer gravitativen Massenabstoßung für sehr kleine Abstände von einer Punktmasse bzw. sehr, sehr große Massen, wie z.B. das Universum.
Anlage 3 zeigt das Programm zur numerischen Berechnung eines Anteils an der rel. Periheldrehung des Merkurs, wie er sich aus der modifizierten Schwerkraftauffassung ergibt (Virtual Pascal v2.1). Das Ergebnis liegt bei ca. –7“. In Anlage 4 wird die Toleranz des Ergebnisses aus dem zugrunde gelegten Berechnungsintervalls von 0,1 Sekunden bestimmt sowie genaue Zahlenwerte für den Größt- und Kleinstwert angegeben. Es zeigt sich der Verdacht, dass die Diskrepanz zwischen Einsteins und Orlovs Berechnung genau geschlossen wird.
Vor diesem Hintergrund kann die Möglichkeit einer natürlichen Massenabstoßung auch für kosmologische Betrachtungen ins Kalkül gezogen werden (z.B. Dunkle Energie).
Desweiteren wird versucht, am Beispiel der Kreisbewegung ein allgemeingültiges Gesetz zu formulieren. Die Zentrifugalkraft wird mithilfe des Ehrenfest’schen Paradoxons zur Probe auf dieselbe Art und Weise entwickelt wie die Schwerkraft (Anlage 5).
Das Gesetz erhält
folgende Gestalt: